ボーア確率

Bohr probability

Bohr probability
大人気ポケモンの ラプラス が駒沢オリンピック公園で捕獲されました。
ラプラスを捕獲したのはこのトレーナーです。
ラプラスを欲しいというプレイヤーがたくさんいたので、公平な方法でひとりを選び、このラプラスをあげることになりました。
公平な方法で多くのプレイヤー達の優先順位が決められました。
優先順位の1番から順番に次の モンティホール問題 Monty Hall problem に挑戦し、最初に正解したプレイヤーがラプラスをもらえることになりました。
その問題は次のようなものでした。
ぜひ自分で解いてみましょう。
問題の意味がよくわからないという方のために具体的な例を2つ示します。
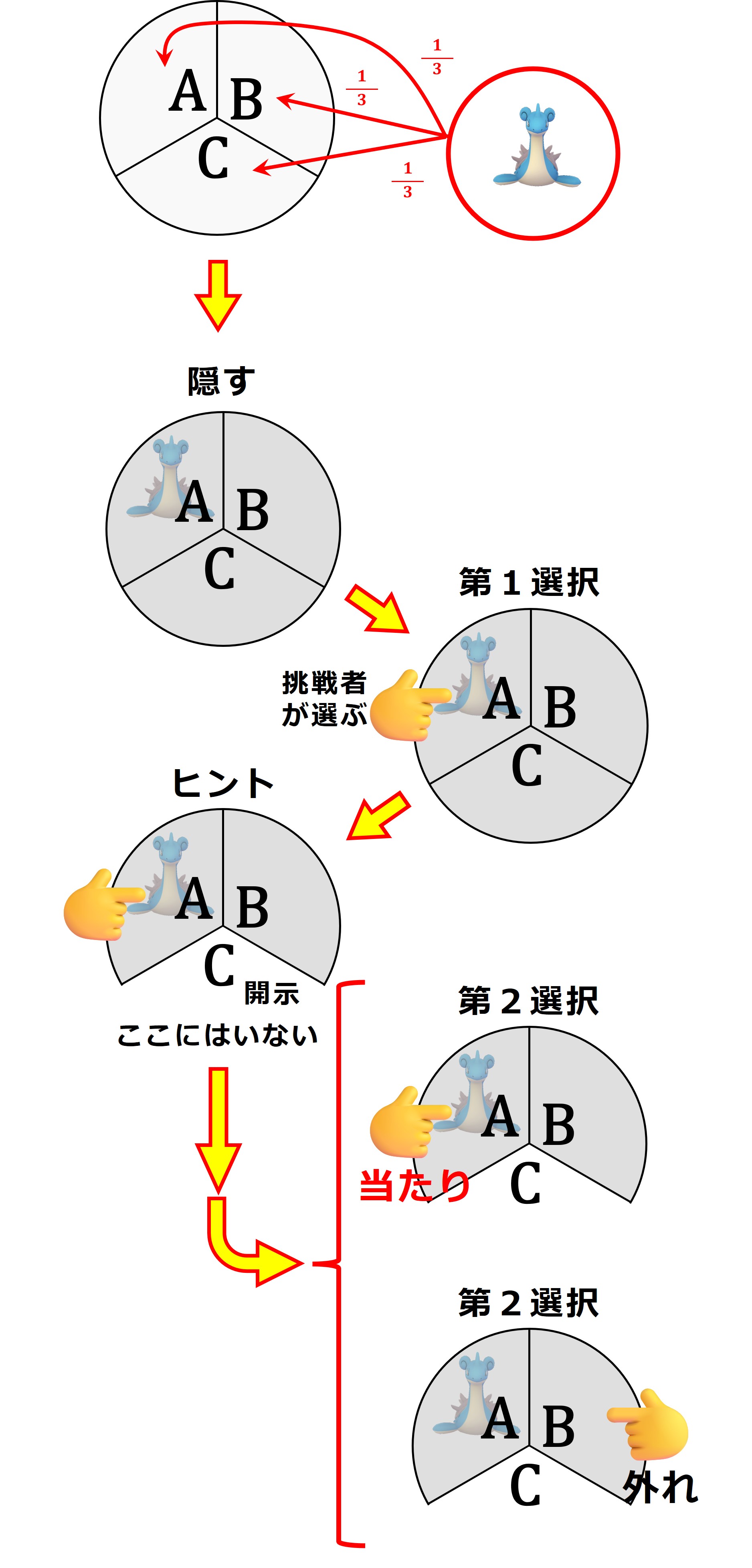
上図(1つめの例)の説明です:
次は2つめの具体例です。今度は B にラプラスを隠します。

上図(2つめの例)の説明です:
この問題で問われている課題の内容をよく理解できたでしょうか。
ぜひ、自分の答えを用意してから説明を読み進めてください。
圧倒的に多くの人が、細かく計算しないで直観的にこの問題を解くときは、次のように考えます。
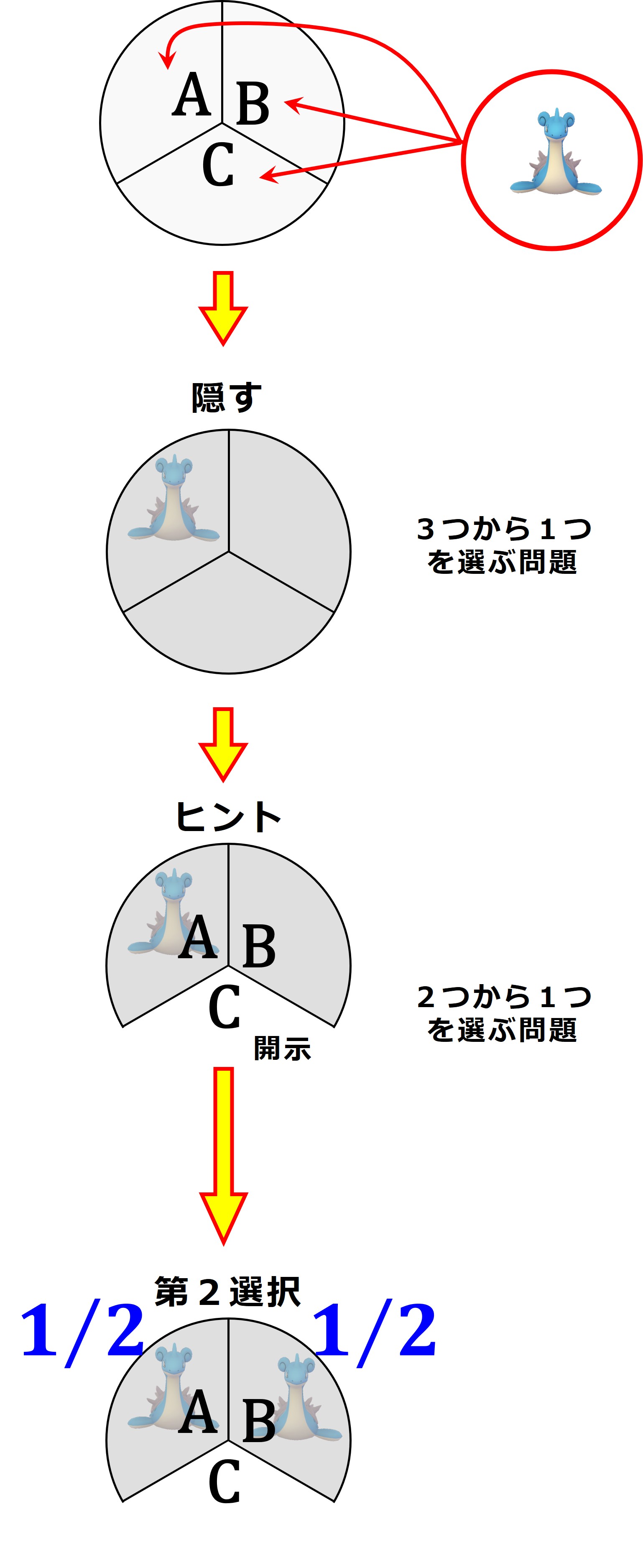
しかし、現代のマクロ確率論に基づく正解は「第2選択では、最初に選ばなかった小部屋に変えるとラプラスの当たる確率が2倍になる」というものです。 🤯 😮 😠
起こる事象の出現確率を計算しながら順を追って見ていきましょう。
まず、起こりうる全事象の種類は「隠す3種類」✕「第1選択の3種類」✕「ヒント開示の1種類~2種類」✕「第2選択の2種類」の最大 36 種類となります。
では「隠す」から始めます。ラプラスは3つの小部屋{A, B, C}にランダムに割り振られますから、実際に A に置かれる確率は 1/3 です。同様に、他の小部屋についても確率は 1/3 です。
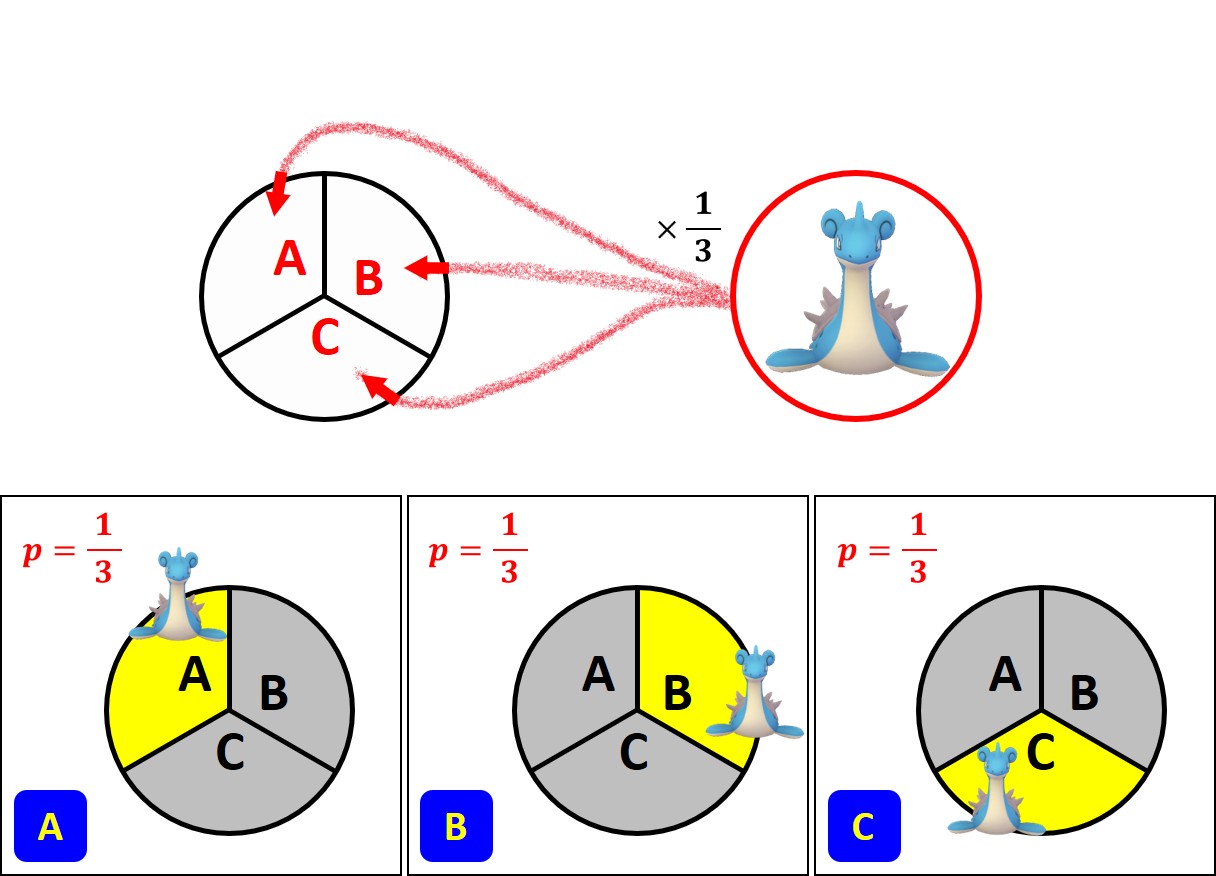
挑戦者による 第1選択 もランダムにおこなわれます。{A, B, C}の小部屋のうち、どの小部屋を選ぶ確率も 1/3 です。
次図は 挑戦者が小部屋 A を選んだ ものとしています。
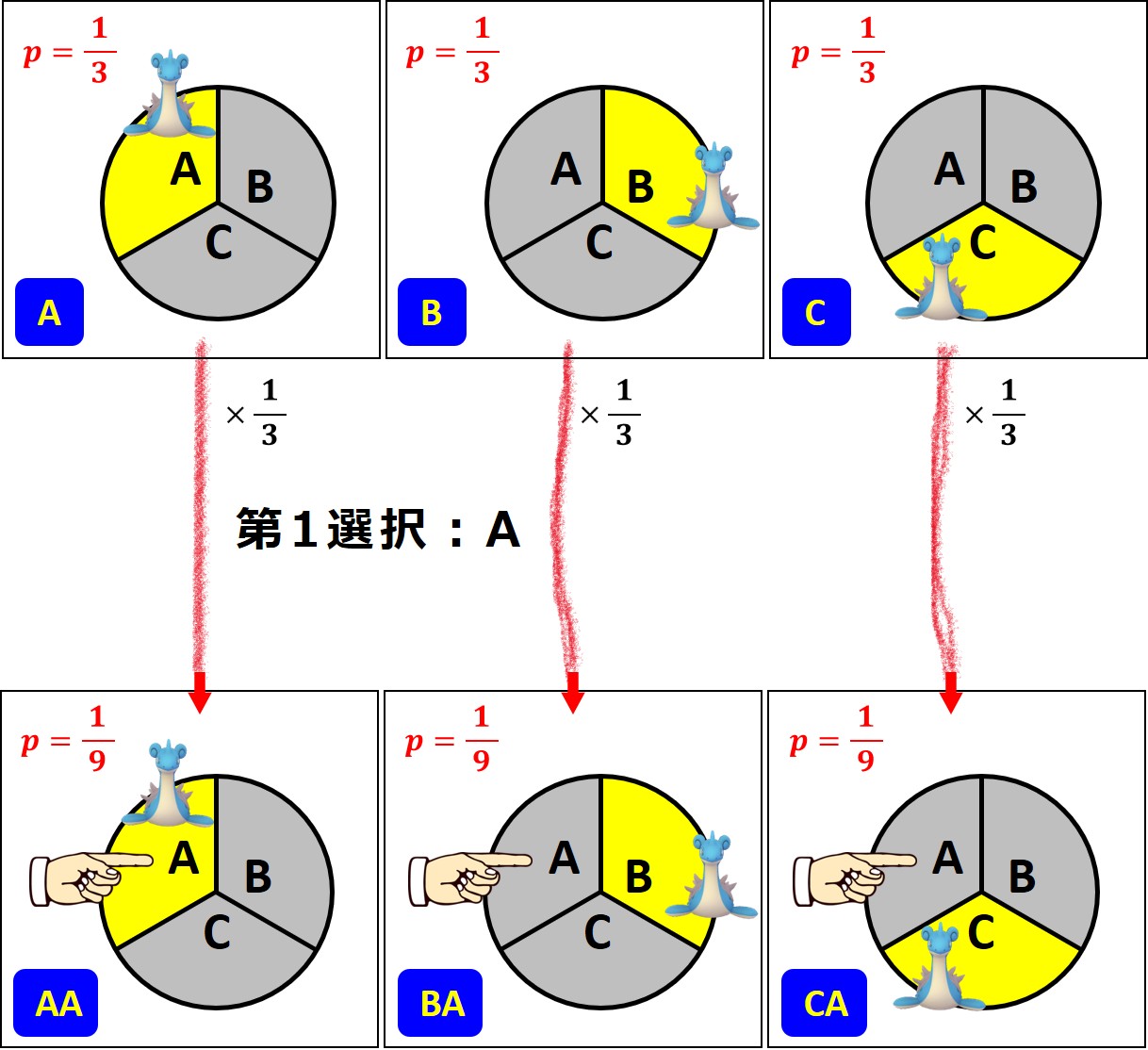
赤字の P = 1/9 は、各事象の起こる確率を示しています。
「ラプラスが A に置かれて、挑戦者が A を選択するという事象」の起こる確率は 1/9 、「ラプラスが B または C に置かれて、挑戦者が A を選択するという事象」の起こる確率は 2/9 だということです。
挑戦者が小部屋 B を選んだ 場合も、小部屋 C を選んだ 場合も同様です。
{A, B, C}の各々について、第1選択が行なわれた時点で、「当たり」が 1/9 、「ハズレ」が 2/9 となります。
では、「ラプラスが A 、挑戦者の第1選択が A 」の場合から出発して、このときに出題者が開示するヒント2種類(C を見せる場合と B を見せる場合の2種類)と挑戦者の第2選択の分岐図を示します。
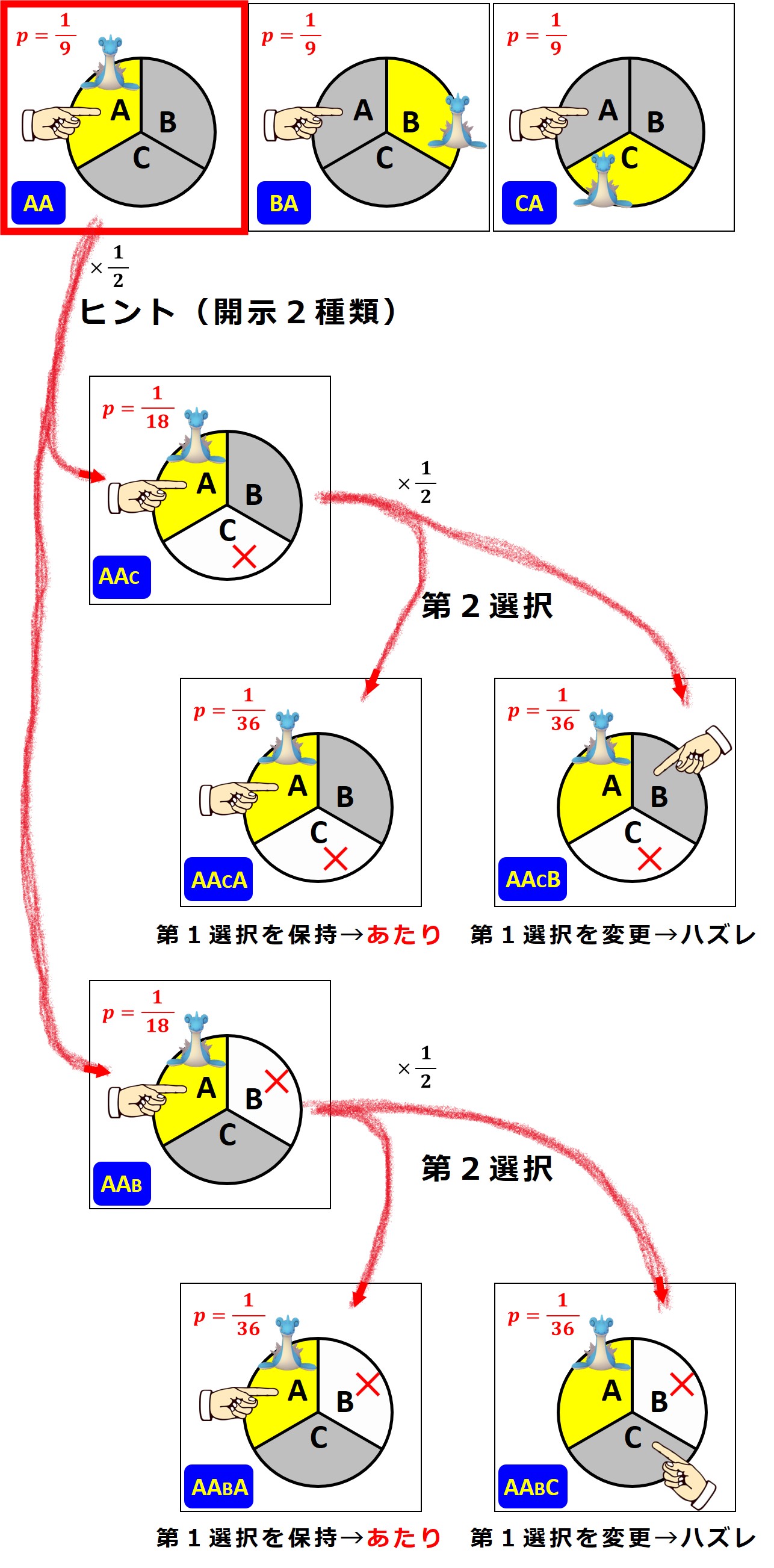
次は、「ラプラスが B 、挑戦者の第1選択が A 」あるいは「ラプラスが C 、挑戦者の第1選択が A 」から出発する分岐図を示します。
ラプラスは、挑戦者が第1選択で選んだ A にはおらず、選ばれなかった B または C にいるので、出題者によるヒント(空の部屋の開示)はラプラスのいない C または B の1種類のみとなります。
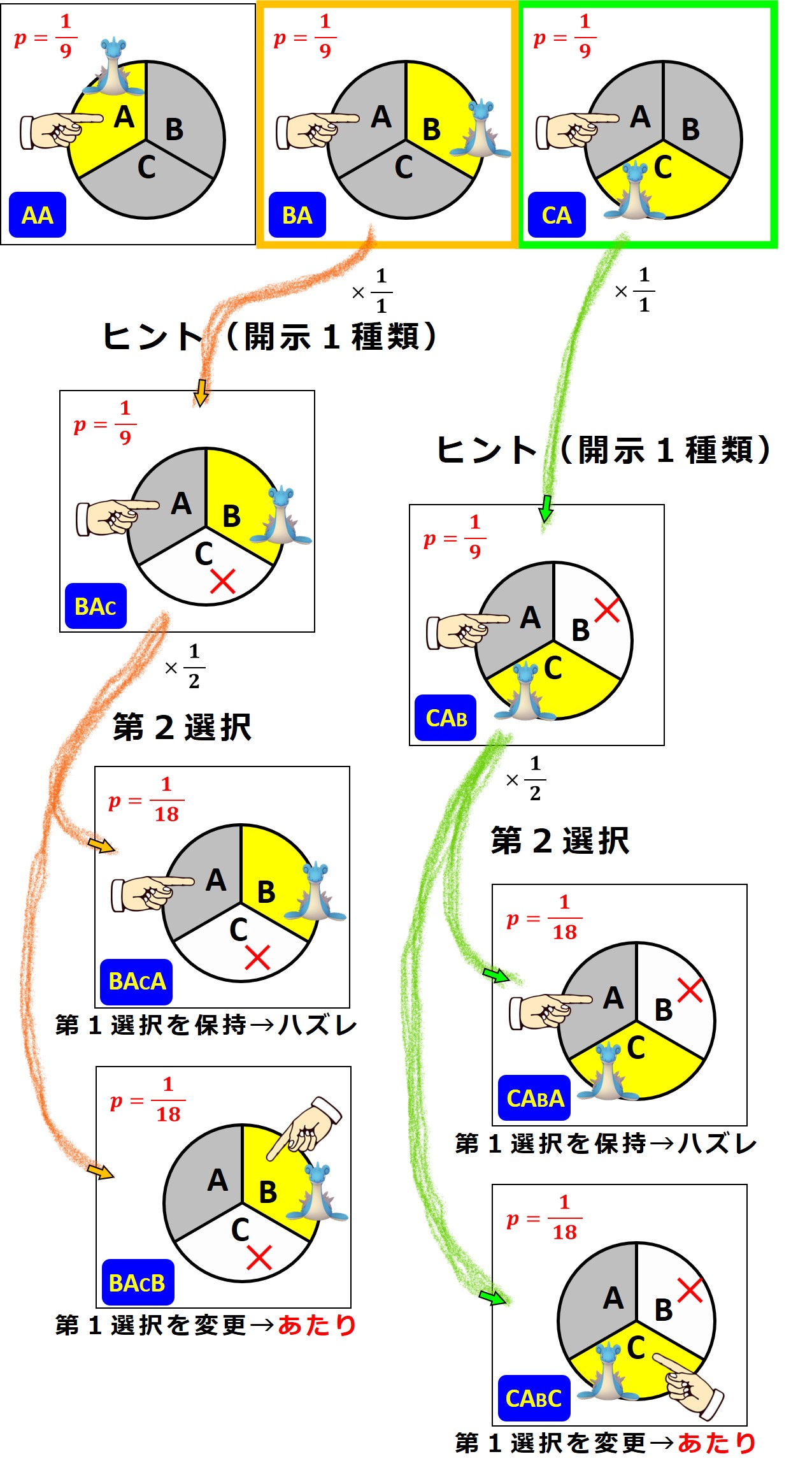
では、当たる全確率を比較します。
「挑戦者の第1選択が A の場合」、「第2選択でも A の選択を保持した場合」にラプラスの当たる確率は
1/36 + 1/36 = 2/36
「挑戦者の第1選択が A の場合」、「第2選択で選択を変更した場合」にラプラスの当たる確率は
1/18 + 1/18 = 2/18 = 4/36
「最初の選択 A を変更しないとラプラスの当たる確率が 1/2 になります」
「最初の選択 A を変更するとラプラスの当たる確率が2倍になります」
挑戦者の最初の選択が B あるいは C の場合も、最初の選択が A の場合と等価ですから、どの部屋を最初に選択しようとも、出題者のヒントを得たあとの第2選択では部屋を変えるのがよいということになります。
挑戦者の第1選択{A, B, C}ごとの確率の合計も計算しておきましょう。
「挑戦者が選択を変えない場合」は
2/36 ✕ 3 = 6/36 = 1/6 < 1/3 ・・・なんと第1選択時の確率より小さくなっています。
「挑戦者が選択を変える場合」は
4/36 ✕ 3 = 12/36 = 1/3 ・・・第1選択時の確率と同じです。
第1選択時に当たる確率 1/3 と比較すると、「第2選択時に選択を変えることで確率が上がる」というよりも「第2選択時に選択を変えないと確率が下がる」といった方が正確な表現になります。
以上の詳細な図説を簡略にしてみます。
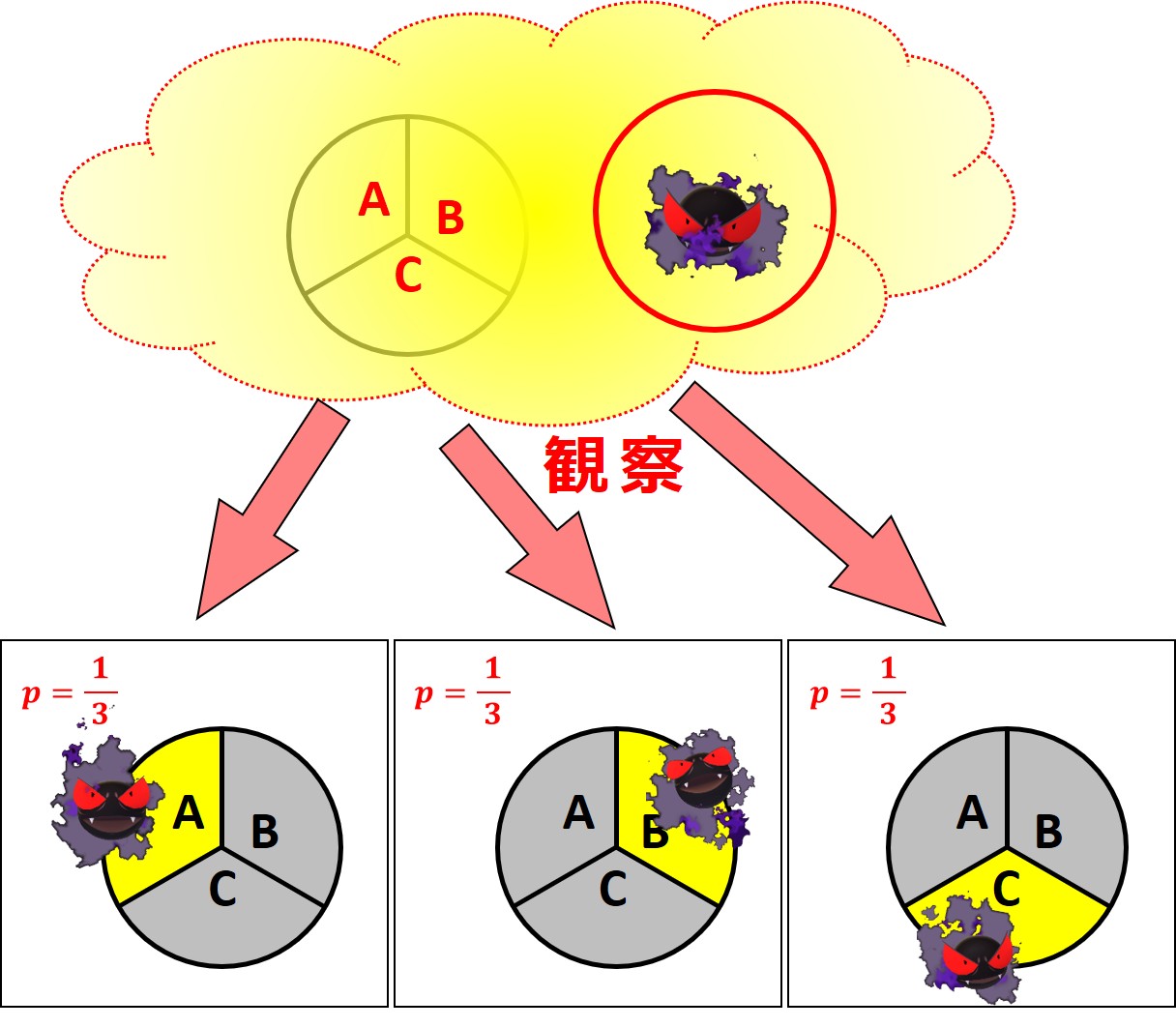
次図の最上段に3つの場合を描いています。ラプラスが{A, B, C}にいる確率はそれぞれ 1/3 です。
最初に挑戦者が A を選んだとしています。簡略図の下段には「当たる場合」のみを示しています。
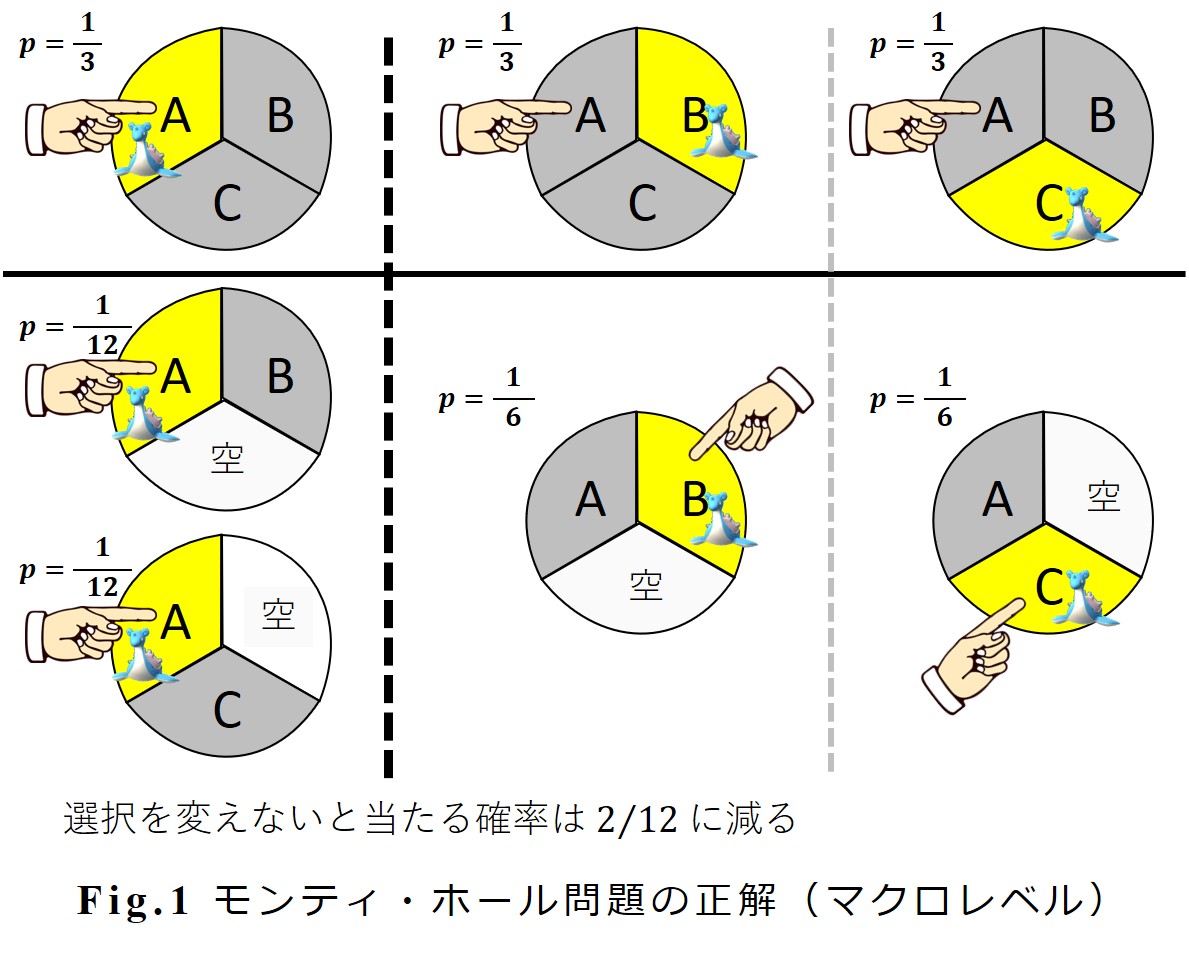
図の下段部分を左から説明します。
ラプラスが A にいる場合(確率は 1/3)、出題者は B または C をランダムに選んで(各々の確率 1/2)開き、ラプラスがいないことを見せることになります。
次に、挑戦者は選択を変えるか、変えないかを決めます(各々の確率 1/2)
これらは等確率ですから、それぞれが起こる確率は 1/3 ✕ 1/2 ✕ 1/2= 1/12 となります。
合計すると 1/12 + 1/12 = 2/12 = 1/6 となります。
ラプラスが B にいる場合(確率は 1/3)、出題者は必ず C を選んで(その確率 1/1)開き、ラプラスがいないことを見せることになります。
次に、挑戦者は選択を変えるか、変えないかを決めます(各々の確率 1/2)
したがって、ラプラスが B にいる場合、挑戦者が A という最初の選択を捨てると 1/3 ✕ 1/2 = 1/6 の確率でラプラスを当てることになります。
ラプラスが C にいる場合も同様にして、挑戦者が A という最初の選択を捨てると 1/3 ✕ 1/2 = 1/6 の確率でラプラスを当てることになります。
したがって、ラプラスが B または C にいる場合、挑戦者が A という最初の選択を捨てると 1/6 + 1/6 = 2/6 = 1/3 の確率でラプラスを当てることになります。
どうでしょうか。納得できたでしょうか。
表で考えるのが好きな方もいます。
あらゆる場合を表にすると次表のようになります(ここに示すのはひとつの例です:自分好みの表を作って確かめましょう)。
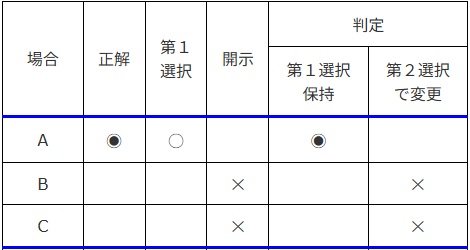
表の一番上の{A, B, C}の3行では、「ラプラスを A に隠した(正解)」、「最初に挑戦者は A を選択した(第1選択)」、「出題者は B または C の小部屋を開けてラプラスがいないことを見せた(開示) 」、「第2選択でも挑戦者が A を保持した場合は当選するが、第2選択で挑戦者が C または B へ変更したときはハズレる(判定)」を意味しています。
| 場合 | 正解 | 第1 選択 |
開示 | 判定 | |
| 第1選択 保持 |
第2選択 で変更 |
||||
| A | ◉ | ○ | ◉ | ||
| B | ✕ | ✕ | |||
| C | ✕ | ✕ | |||
| A | ◉ | ◉ | |||
| B | ✕ | ✕ | |||
| C | ✕ | ||||
| A | ◉ | ◉ | |||
| B | ✕ | ||||
| C | ✕ | ✕ | |||
| A | ✕ | ✕ | |||
| B | ◉ | ◉ | |||
| C | ✕ | ||||
| A | ✕ | ✕ | |||
| B | ◉ | ○ | ◉ | ||
| C | ✕ | ✕ | |||
| A | ✕ | ||||
| B | ◉ | ◉ | |||
| C | ✕ | ✕ | |||
| A | ✕ | ✕ | |||
| B | ✕ | ||||
| C | ◉ | ◉ | |||
| A | ✕ | ||||
| B | ✕ | ✕ | |||
| C | ◉ | ◉ | |||
| A | ✕ | ✕ | |||
| B | ✕ | ✕ | |||
| C | ◉ | ○ | ◉ | ||
| ◉○数 | 9 | 3 | 3 | 6 | |
| ✕数 | 18 | 6 | 12 | 6 | 6 |
表の一番下のほうに「○✕の集計」をしていますが、ヒントを受けた挑戦者が選択する小部屋を変更した場合は、第1選択を変えないで保持した場合の2倍当選しています。
他の解説も見てみましょう。
◆ モンティ・ホール問題とその解説(難波博之, 高校数学の美しい物語, 2021.03.07):▶ ▶ ▶
◆ ウィキペディア(:▶ ▶ ▶)
さて、モンティ・ホール問題では、「数学的で合理的な説明が正しく、人間の直観的な確率感覚は間違っている」とされてきました。
しかし、私は、「多くの人々が感じる直観的な確率こそが、現実の物質世界を支配している確率なのではないだろうか」と考えました。
つまり、モンティホール問題を間違えるような直観的な確率感には、何らかの物質的な根拠があり、ある条件のもとにおいてはそのような直観的確率が正しいと考えました。
その考え方を紹介します。
登場するのは子供たちに大人気の量子ポケモン「ゴース」です。
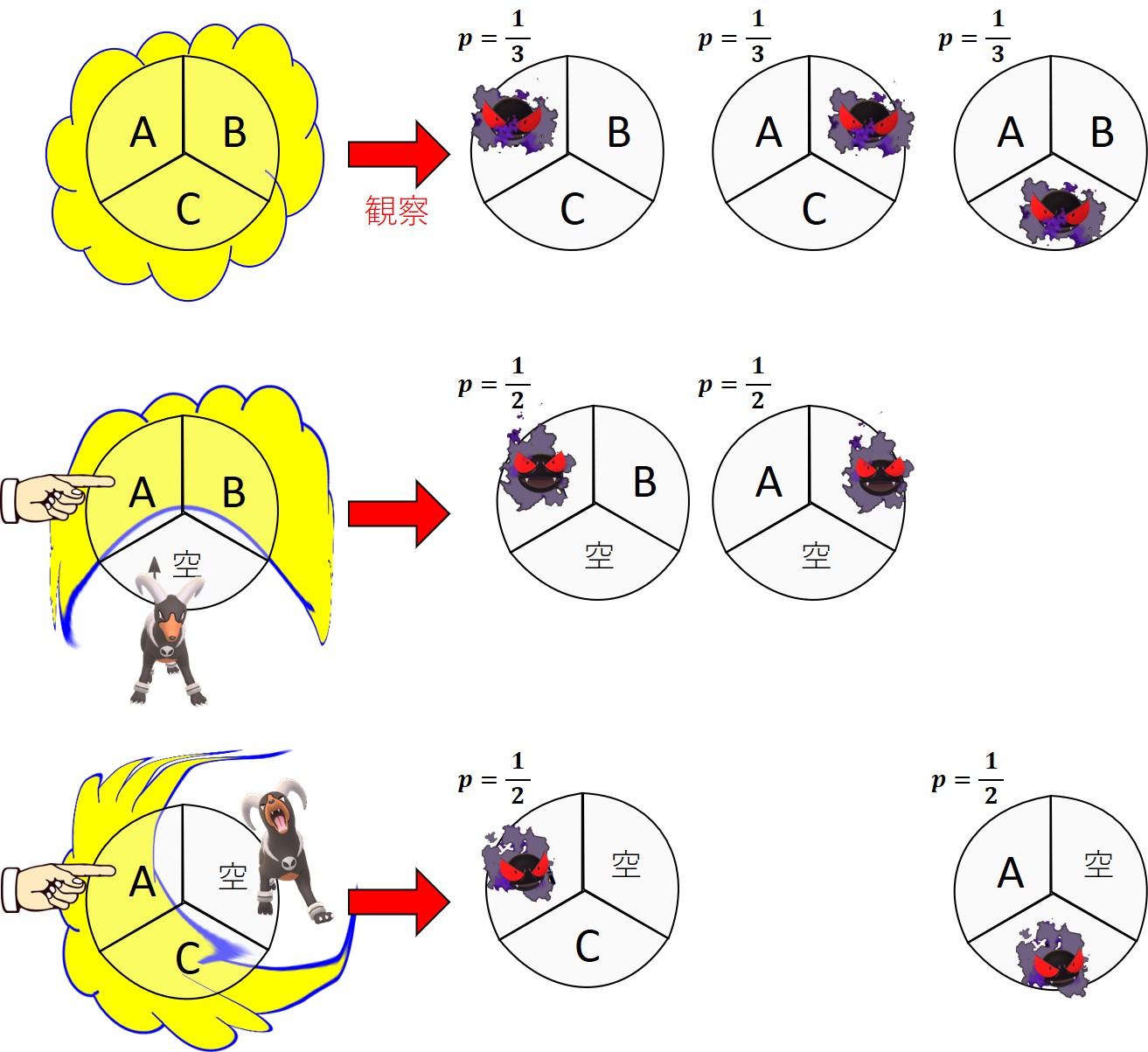
量子ポケモン「ゴース」はどこにいるのかわからない、というか、どこにでもいるのですが、観察すると特定の位置に姿が現れます。
ゴースを使ったモンティホール問題は、次のようなものになります。
正解は、人間の直観的な確率感に基づくものとなります。第1選択を保持しようが、変えようが、確率は同じです。
ラプラス Lapras の示したマクロ世界の数学的確率を「ラプラス確率 Laplace probabirity」、ゴース Gastly の示したミクロ世界(量子世界)の確率を「ボーア確率 Bohr probability」と呼ぶことにします。
エントロピーのもとになっているのは、ボーア確率ではないだろうかと私は目をつけています。
「エントロピー:その形式的呪縛からの解放」(2016.09.28):▶ ▶ ▶
(Fig.1の確率表示が間違っています:このウェブページの図が正しいです)
モンティ・ホール問題において示される人間の直観的な確率感は、量子力学的な根拠を持っているのだろうという仮説に基づいてミクロレベルで確率の正体に挑戦し始めました。
「ロジャー・ペンローズ」や「量子脳理論」について調べてみてください。
モンティホール問題でみんなが同じような間違いを犯すということは、共通の物質的根拠があるということです。
しかもこのボーア確率は、エントロピーの正体を明らかにするカギになっていると考えられます。
しかし、その後のコロナ騒動で私は免疫学の世界に引き戻されました。
令和8年2025年1月に、ようやく平成28年(2016年)のスタート位置に戻ることができました 😄
しかし、途方に暮れています。
深い霧に覆われた林の小道を歩いています。

霧が晴れると、高さ数百メートルの断崖絶壁に阻まれていました。

Home:▶ ▶ ▶