医者の不養生:一喜一憂しない血圧管理
先に見たページに戻るときは、リンクを使うよりも、ブラウザの「<(もどる、Back)」を使うと通信量を節約でき、また早く表示されます。
では、「医者の不養生:一喜一憂しない血圧管理」の理論的な部分を説明します。
血液は、生命活動の源である 栄養や酸素 を細胞まで運び、細胞からは不要になった 熱や二酸化炭素・代謝産物等 を受け取って、再利用や破棄処分のために肺や肝臓・腎臓といった臓器まで運んでいます。
細胞の生命活動に必要な物質を細胞に届け、不必要な物質(溜まると有害な物質)を細胞周囲から取り除いているのが血液です。
ここで特に知りたく、また臨床においてもわりと簡易な方法で知ることができるのは、脳や心臓、また肝臓や腎臓といった臓器に きちんと必要十分な量の血液が流れて生命活動が営まれているかどうか です。
知りたいのは十分な量の血流があるかどうか(つまり血流量)であって、血圧ではありません。
血圧は上がったり下がったり変動していますが、同時に血管抵抗(:血流を妨げるもの)など他の要素も大きくなったり小さくなったり調整されていて、血流量としてはほぼ一定を保たれている と考えられます。
組織の代謝活動が一定のとき、栄養や酸素に対する需要も一定です。心臓や血管を支配する神経は、心臓の働きや血管壁の緊張状態を微調整して組織の血流量を一定に保っています。
その調整の範囲内で血圧や血管抵抗は、お互いに絡み合うように変化しながら一定の血流量が維持されているのです。
そこで、この血流量調節の仕組みを理解しておけば、血圧の変動だけでオロオロとうろたえることも無くなると期待できます。
そして生理的変動の範囲内であると理解して無視していてよい血圧変動と、ちょっと注意しなければいけない病的血圧変動を区別できるようになるでしょう。
また必要以上に血圧を急激に下げすぎて脳梗塞をおこすような危険を避けることもできるでしょう。
そこで、かなり乱暴な方法となりますが、長い管を流れる 液体の流量についての物理法則 や 液体の状態方程式 などを利用して、血流量調節の仕組みの実用的な理解を試みます。
高度の思考力を要する難しい話はいっさい出てきませんが、「分数計算の知識(基本は、かけ算とわり算)」、「近時記憶力」、「根気」が必要です。
さて、心臓を出た動脈は、どんどん枝分かれ(分岐:ぶんき)をしていきます。
分岐前の血管半径よりも分岐後の血管半径は小さくなりますが、血管の断面積の合計は分岐後が大きくなっていきます。
しかしここでは、そうした動脈の特徴は無視して、太さの変わらない1本の長い真っ直ぐな管だと仮定します。
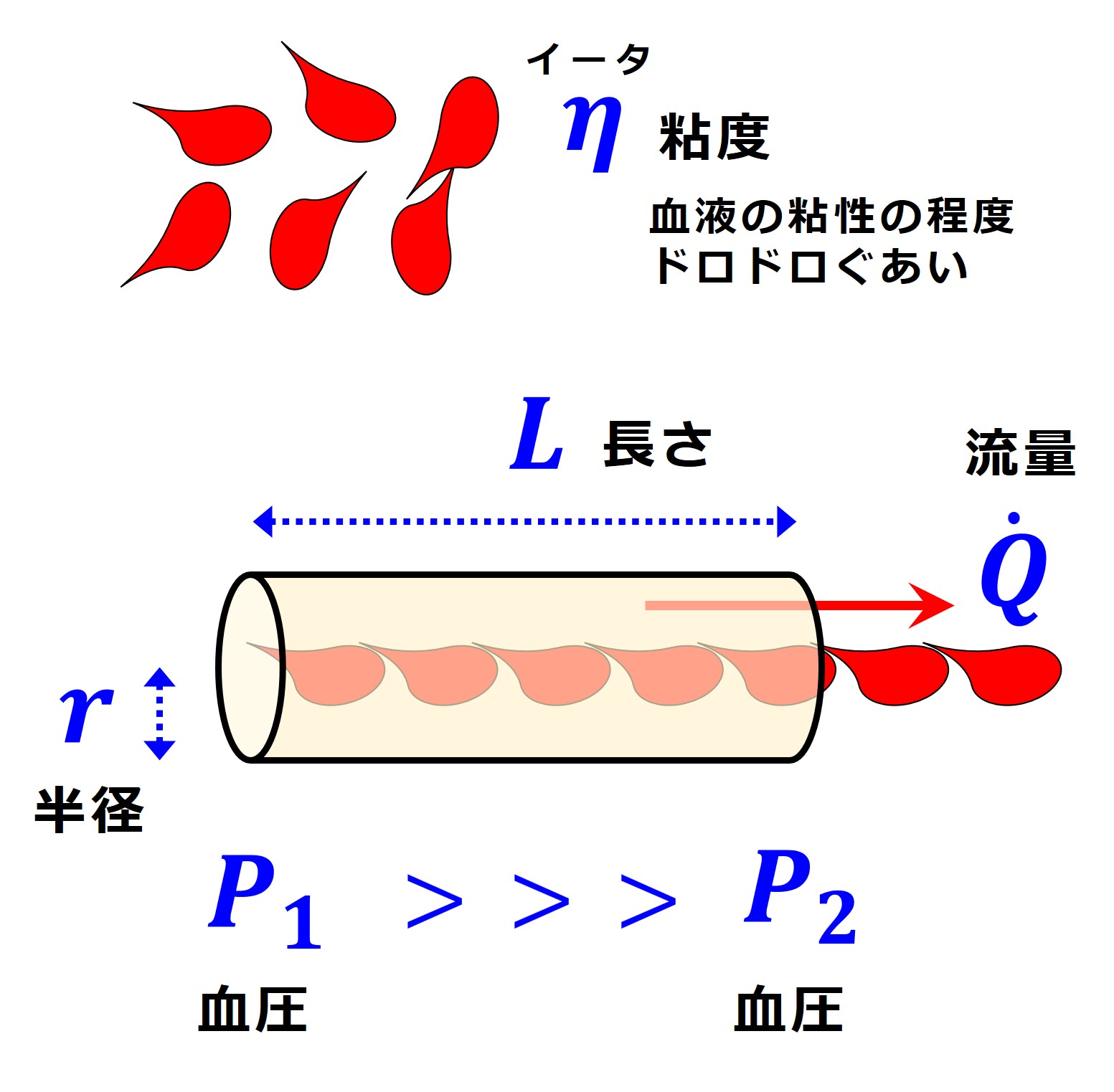
太さは変わらず、半径を r とします。
長さも一定であり、長さを L とします。
また実際の血液は水とアルブミン、ブドウ糖、赤血球など大小さまざまな要素から構成されていますが、これもただの水のように考えておきます。
水道水など、管の中を乱れないで真っすぐに流れる液体(層流)の流量について、ハーゲン・ポワズイユの法則 というものがあります。
それを血管内(動脈内)の血液の流れに応用します。


もちろん、この数式を覚える必要はありません。ハーゲン・ポワズイユという名前も覚える必要はありません。(ゴットヒルフ・ハインリッヒ・ルートヴィッヒ・ハーゲン はドイツの技術者で1839年に法則を発見、ジャン=ルイ=マリー・ポアズイユ はフランスの物理・生理学者で1940年に法則を発見だそうです)
見る必要のない参考です:↓
あくまで 参考(式の導出):【ハーゲン・ポアズイユの式】を解説:層流の圧力損失計算式(2021.02.18、化学工学レビュワー 化学工学系の情報発信ブログ)
あくまで 参考(式の導出):ハーゲン・ポアズイユ流れとは?|理論と導出【流体力学】(2023.01.03、高校物理からはじめる工学部の物理学)
あくまで 参考:ポアズイユの法則と血流【物理オリンピック】(2021.03.22、予備校のノリで学ぶ「大学の数学・物理」)
このような数式とお付き合いしたくないと思われる方も少なくないでしょうが、後でとても簡単な数式に入れ替えていきますので、少し我慢してください。
なお、一時的でかまわないので、文字が何を表しているのか、慣れていない方は覚えてください。
π (パイ)は円周率(3.141592653…)です。
長さ L は Length(ながさ)、半径 r は Radias(半径)、血圧 P は Pressure(圧力)、血液量 Q および血流量 Q の Q は Quantity(量)の頭文字です。
もちろん英語を覚える必要はありません。「文字 → 意味」に慣れて下さい。

Δ(デルタ) は変化量を意味しています。ΔP は圧力の変化量のことです。
注: 血液量(けつえきりょう)はただの Q 、血流量(けつりゅうりょう)は「文字の上に点(ドット)を打った Q 」で区別していますが、ブラウザによってはうまく表示されません(Google の Chrome 等)。

昔の学校教育では体積(容積)に「ℓ(リットル)」を使いました。近年は「L(リットル)」を使うようです。ここでは長さに L を用いており、間違えの原因になるので、基本的に体積の単位には「m3」を用います。「1m3」は1辺1mの立方体の体積です。
粘性 η (イータ)はギリシャ文字(アルファベットの H に対応)です。要するに「ねばりけ」、「血液のドロドロ具合」です。
ハーゲン・ポワズイユの法則 を示す数式を覚える必要はありませんが、各項を個別に大きくしたり小さくしたりして血流量の変化の様子をみておきましょう。
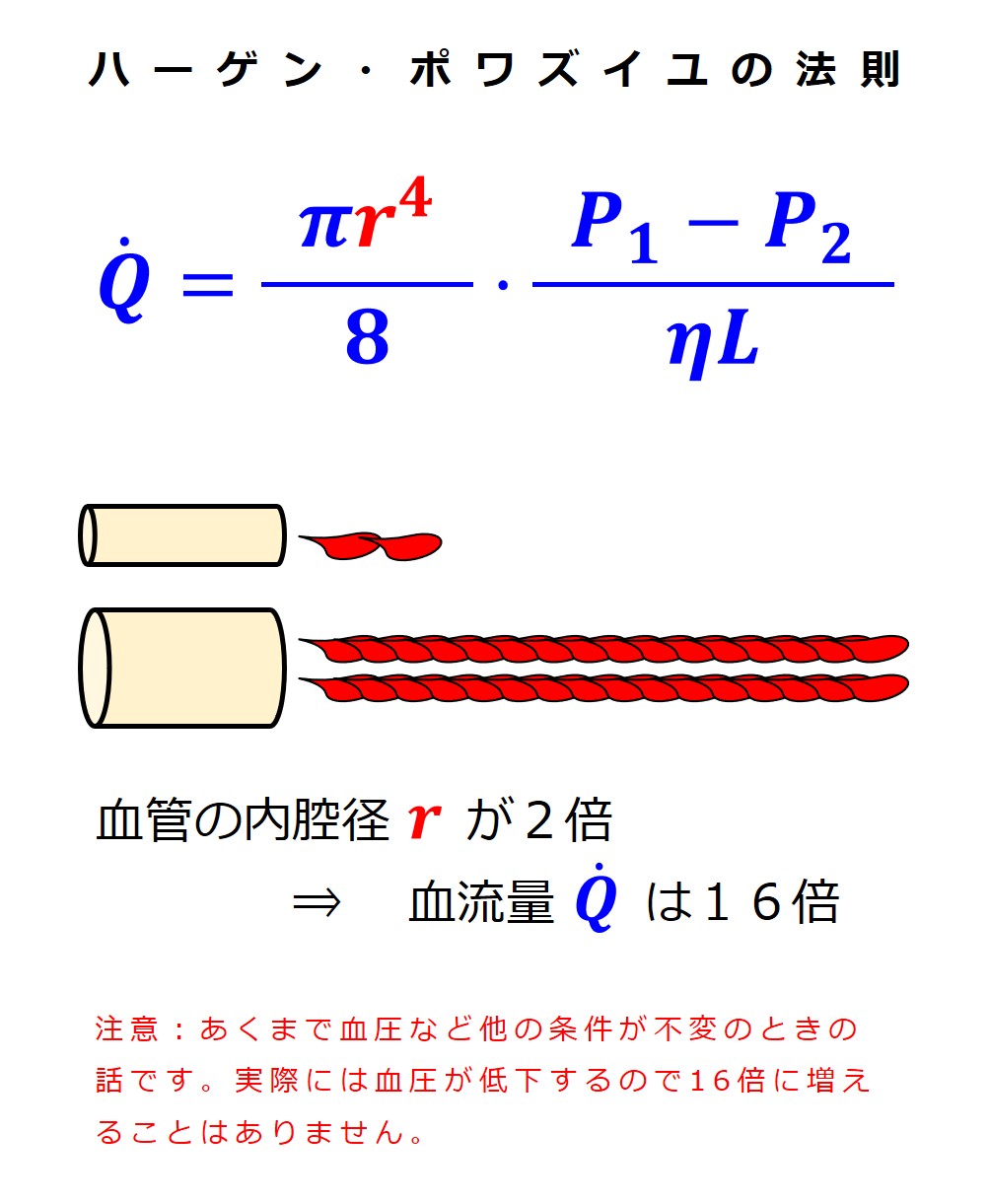
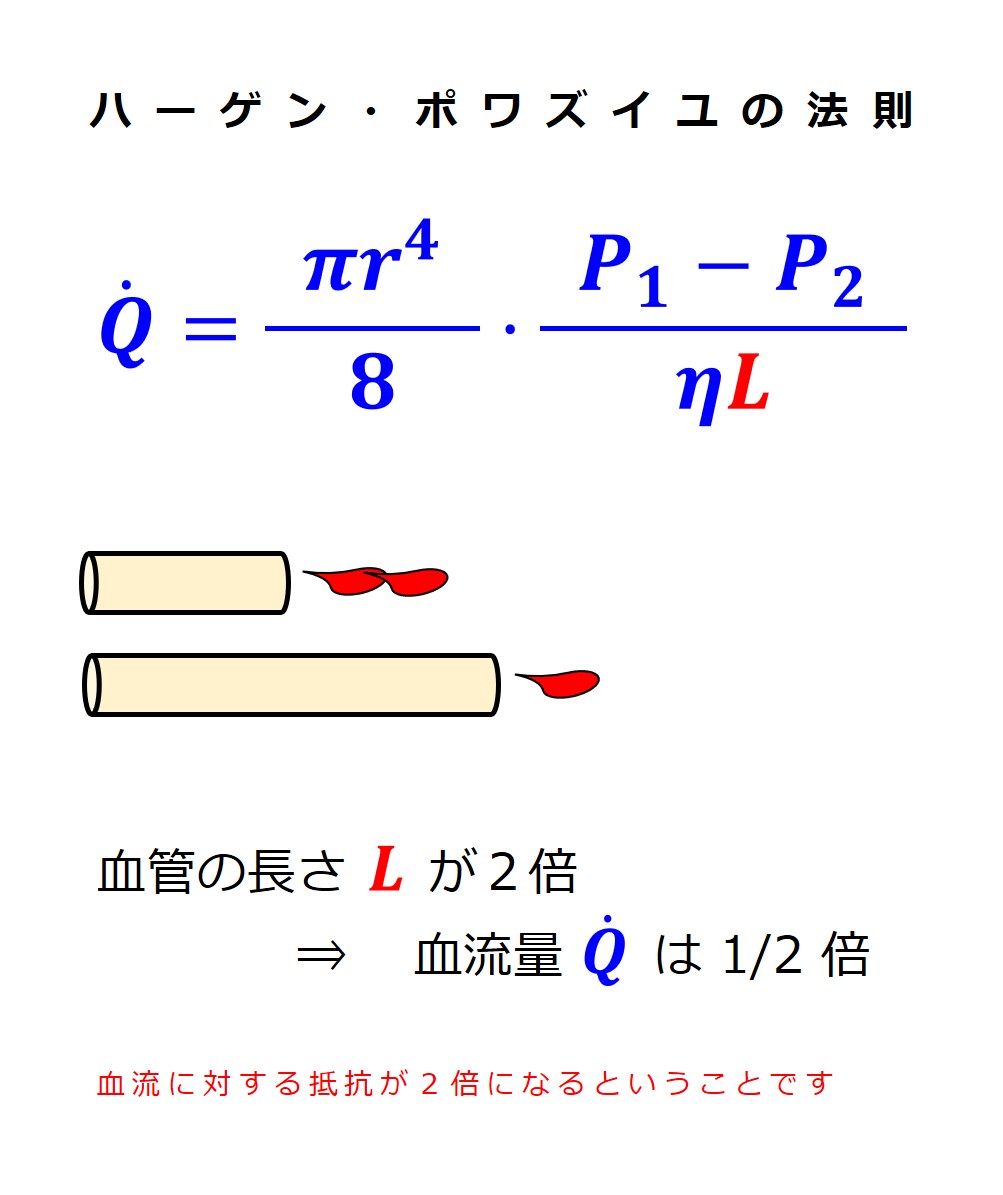
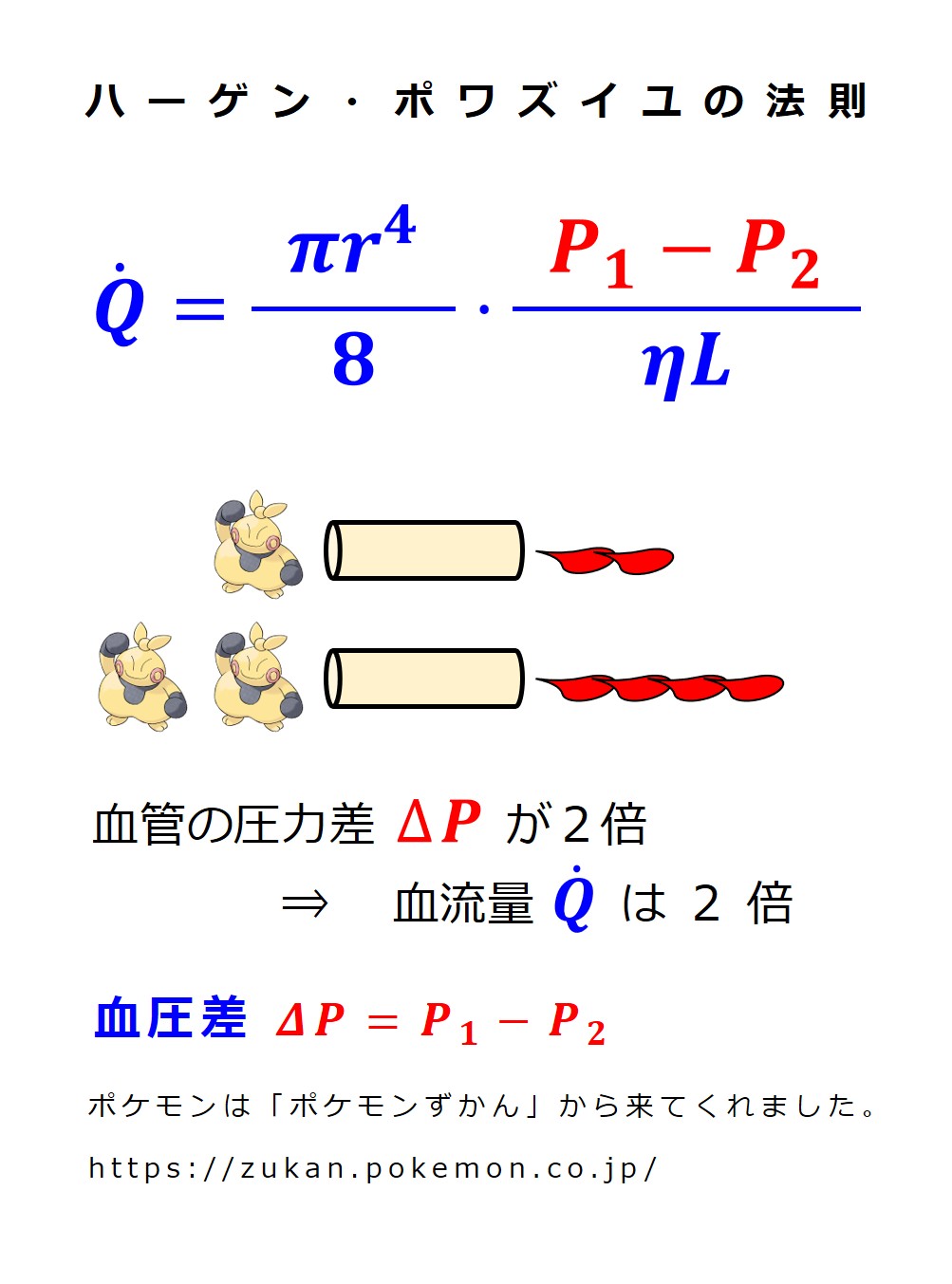
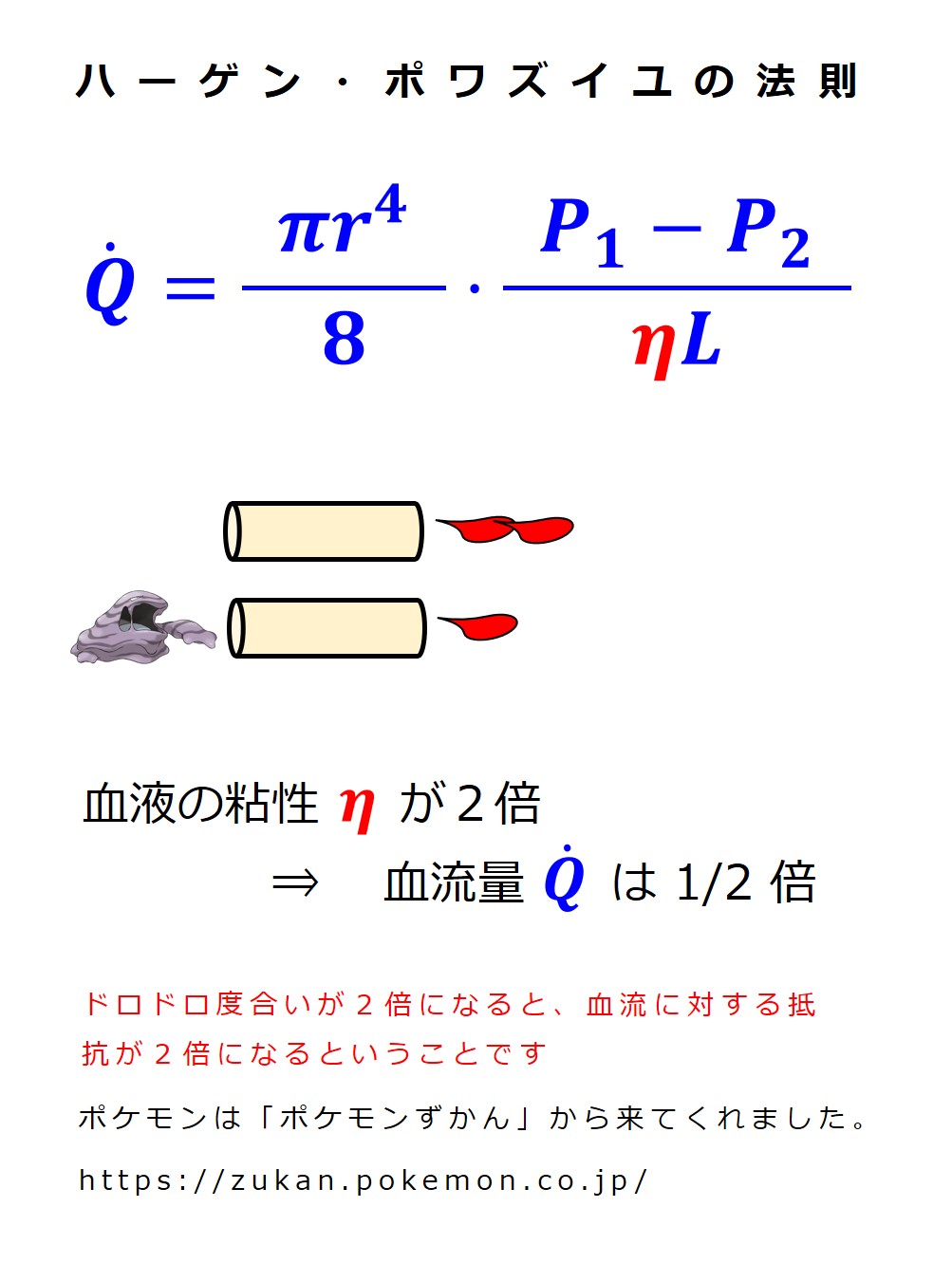
血管半径の変化による影響がすごいですね。
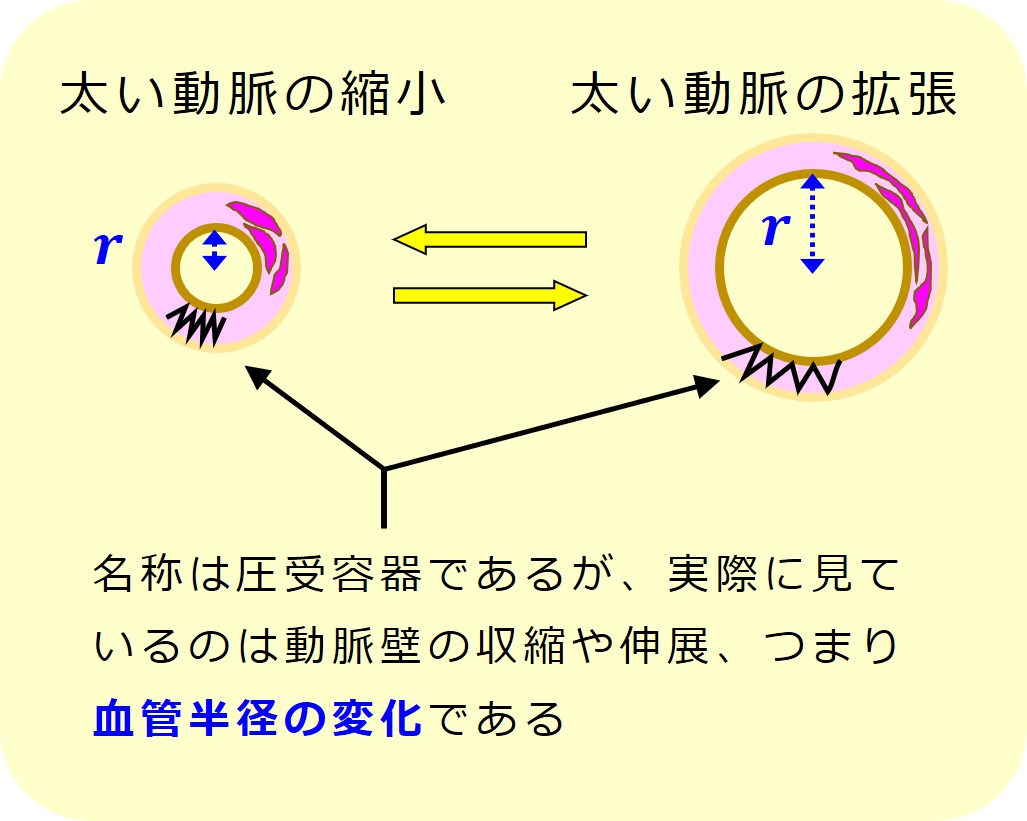
最初に紹介した説明:大動脈弓や頸動脈洞にある「圧受容器」は、実際には圧力を見ているのではなく、血管半径の変化を見ているという説明を思い出してください。
数式を変形して、血液の流れに対する 抵抗 R (Resistance)の候補も見ておきます。
見慣れていない方にはなんだか難しい操作をしているように思えるかもしれませんが、何のことはない、単に「抵抗が大きくなれば流量の落ちることがわかりやすい形」に変形するだけのことです。

血流に対する抵抗の候補 R'' から、1/V を取り出したものが抵抗の候補 R''' です。
なぜそのような余計なことをするのか?
それは、PV という形を作っておくと、液体の状態方程式と絡めることができるようになるからです。これについては、ずっと後の「◆ 数式のバサ切り(2)」で説明します。
もちろん、これらの数式を覚える必要はまったくありません。
「血流を妨げる抵抗の候補です」と数式を示されたとき、ひとつひとつの項目を見て抵抗値の変化を予測できればそれでよいのです。
「ドロドロ血液では抵抗が大きい、管が長いと抵抗が大きい、半径が大きくなると抵抗が激減する、圧力が小さいと抵抗が大きい」と読み取ることができれば十分です。
(理数系などで専門的な勉強をしたことのない)一般の方は、ゴチャゴチャした数式に、ただ慣れていないだけのことです。
「分数計算、忘れてるかも」という方は次図を見て思い出してください。
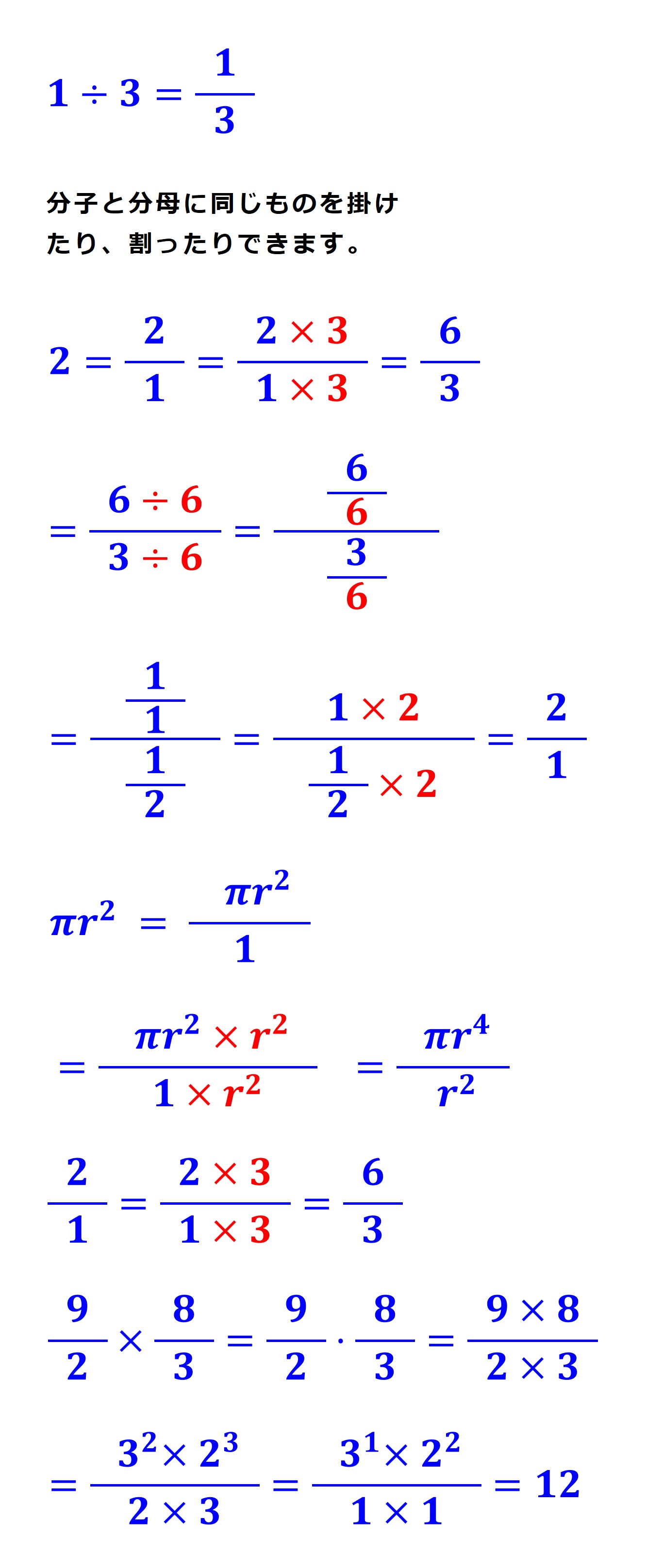
また、次の計算式で円の面積や円柱の体積を求めることができることも確認しておきましょう。
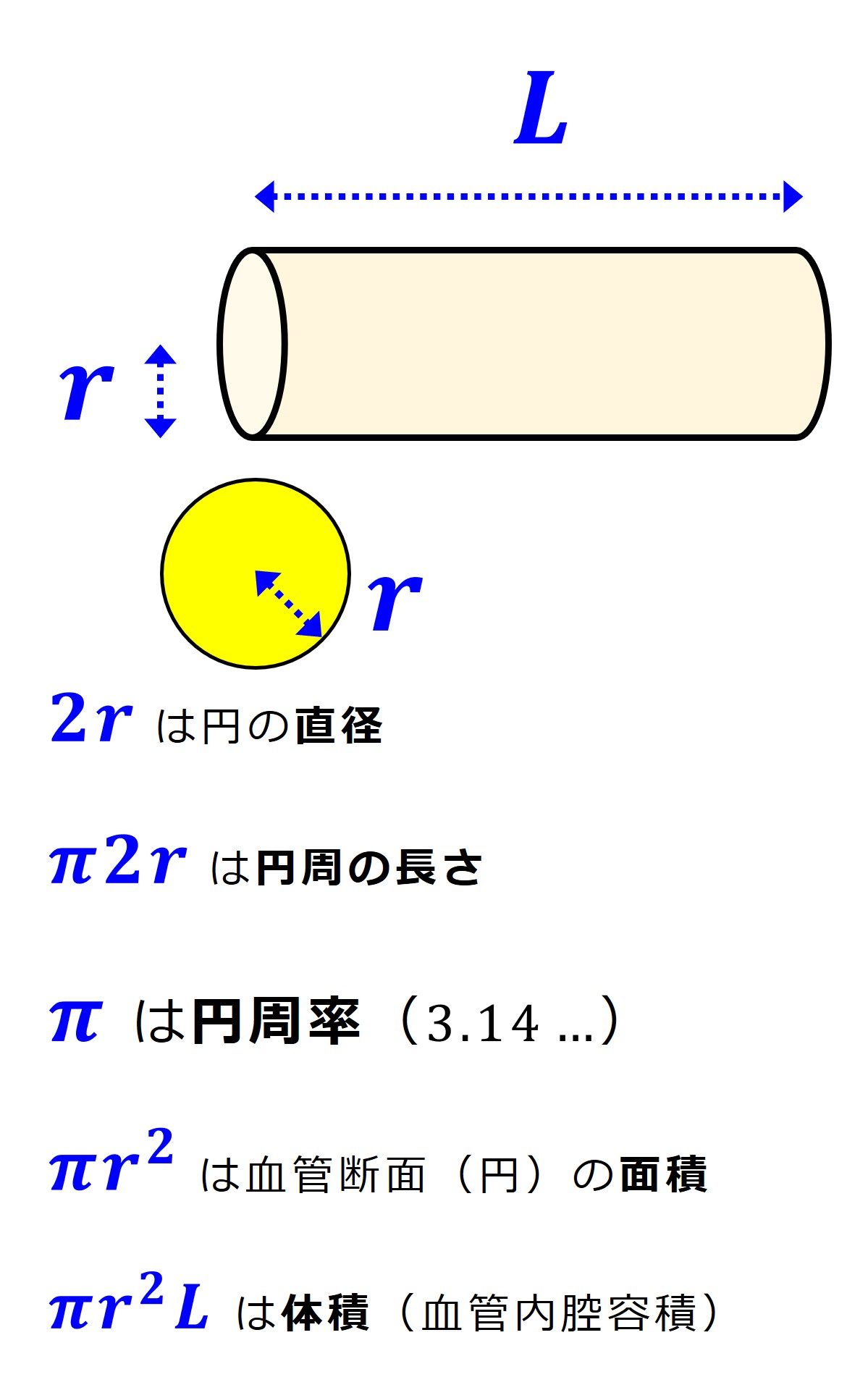
覚えておく必要のある計算式は何もありません。
「そういえば円の周囲の長さと直径との比率(円周率:3.14…)を「パイ」と呼んでいたなぁ」と小学校時代を思い出していただければそれで十分です。
先ほど、血流に対する抵抗の候補を求めるために数式をいじりましたが、結果だけ整理すると次のようになります。
なお、血圧差 ΔP を血圧 P に置き換えています。

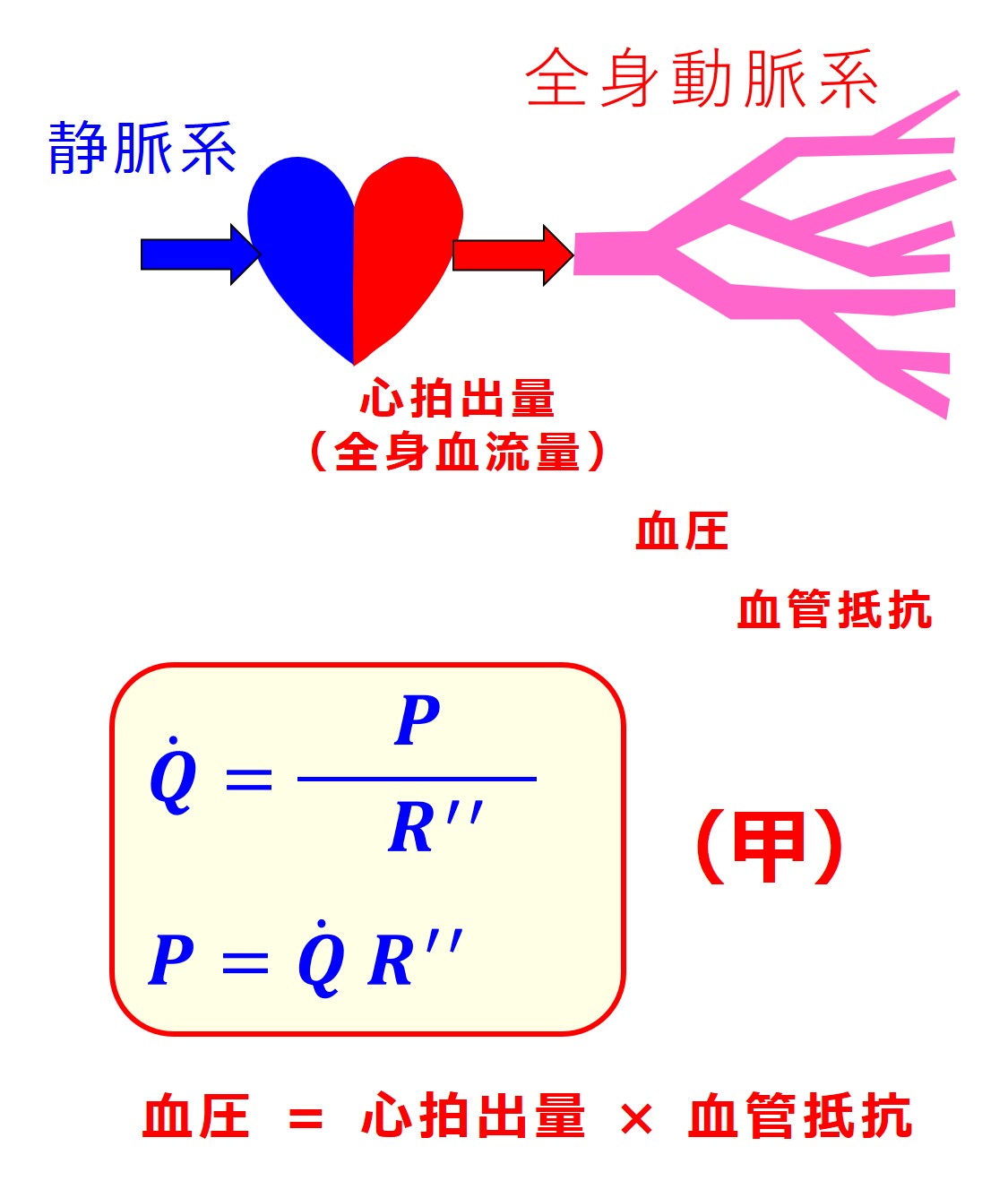
今調べていただく必要はありませんが、「心拍出量 血圧 血管抵抗」といったキーワードでネット検索をかけると出てくるのが「甲式」です(・・・ここでは「乙式」で進むので・・・今調べると、混乱することになるでしょう)。
そこでは「血流量=心拍出量」として「血圧=心拍出量×血管抵抗」という式が出てきます。
循環生理学の基本的な数式として医学生等は覚えます。
しかし、その数式をまる覚えして使っていると「血圧中心の見方」に偏重していく恐れがあります。
しかしここでは「乙式」を中心に見ていくことになります。
冒頭でも紹介しましたように、ヒトの循環器系は血圧を直接モニターしていません。
今後血圧 P を数式から消していきます。
そのためには「乙式」の方が便利なのです。

ここで、今後使うのは「乙式」です。

ここでおこなった抵抗を決めるための数式処理を整理すると次図になります。
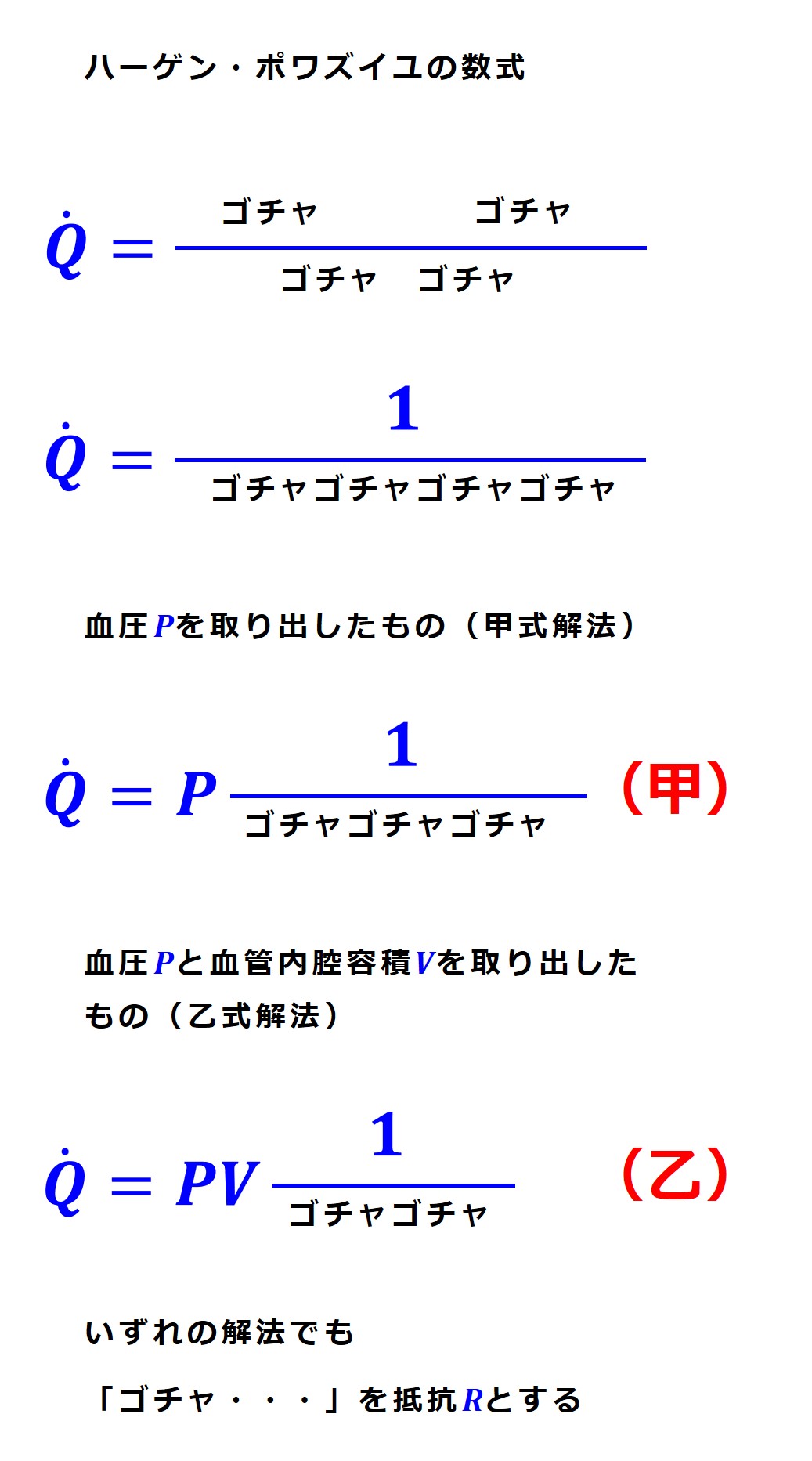
医学生等への注意:式変形過程をみればわかるように「甲式」も「乙式」も本質的には同じものです(ハーゲン・ポワズイユの法則由来)。しかし抵抗 R の意味が両式では異なっています。循環生理の本質をつかんでいくためには「乙式」ですが、資格試験用に覚えるべきは「甲式」です。ここの説明はすべて「乙式」で進めて行きますので注意して下さい。
乙式解法は、かなりマニアックな方法のようです。2024年現在、かなり分厚い生理学の教科書にも載っていません。もしかすると、ふつうはやってはいけない乱暴な操作なのかもしれません。しかし出血性ショックなどの病態の理解に便利なので、私は約30年前の平成7年1995年から(教育でも)使っています。若いころは蘇生を研究対象にやっていたので、使える便利なものは何でも使うようになってしまいました 😅 乙式解法のことを生理学者はみんな知っている、当たり前の解法だと思っていましたが、そうではなかったようです。
ハーゲン・ポワズイユの法則は管の半径が大きくなる時、流速も増えることが前提です。流速が一定ならば、半径が2倍のとき断面積は4倍になるので流量も4倍になりますが、ハーゲン・ポワズイユの法則では、流速も増えて流量が16倍になります。実際の心臓血管系の場合、心拍出量は最大でも5~6倍に増えるのが限界のようです。血管半径の増加で増大した血管床を血液で満たすことができない場合、血圧が下がり、流速も低下します。そのような場合も半径の4乗の効果そのものは出ているのでしょうが、実感できなくなります。「乙式」は「甲式」よりも簡単に適用でき、実感と合うことも多いような気がします。出発点は同じですが、いろいろと調べないと「乙式解法=超おススメ」とは言えません。
先に見たページに戻るときは、リンクを使うよりも、ブラウザの「<(もどる、Back)」を使うと通信量を節約でき、また早く表示されます。
医者の不養生:一喜一憂しない血圧管理
How is this left? Earlier this year Barnaby Cox made the big decision to leave the QS grind and take up a job as a surf coach for Perfect Wave at Kandooma in the Maldives. He’s not looked back! Full feature in the new issue ! pic.twitter.com/gWrIRneIQS
— CARVE Surfing Magazine (@CarveMag) October 6, 2024
Welcome to @kai_lenny’s Big Wave playground 🛝
— World Surf League (@wsl) December 16, 2023
Life of Kai S3 out now on Red Bull TV.@RedBull_Surfing pic.twitter.com/k22me5vscn
Big Wave Season is here and @lucaschumbo is ready 🌊
— World Surf League (@wsl) February 17, 2025
The Tudor Nazaré #BigWaveChallenge is currently on Yellow Alert, with a probable start in the next 48 hours, February 18th.@tudorwatchusa | @redbull | @visitportugal pic.twitter.com/O0ugWHiKBF