医者の不養生:一喜一憂しない血圧管理
先に見たページに戻るときは、リンクを使うよりも、ブラウザの「<(もどる、Back)」を使うと通信量を節約でき、また早く表示されます。
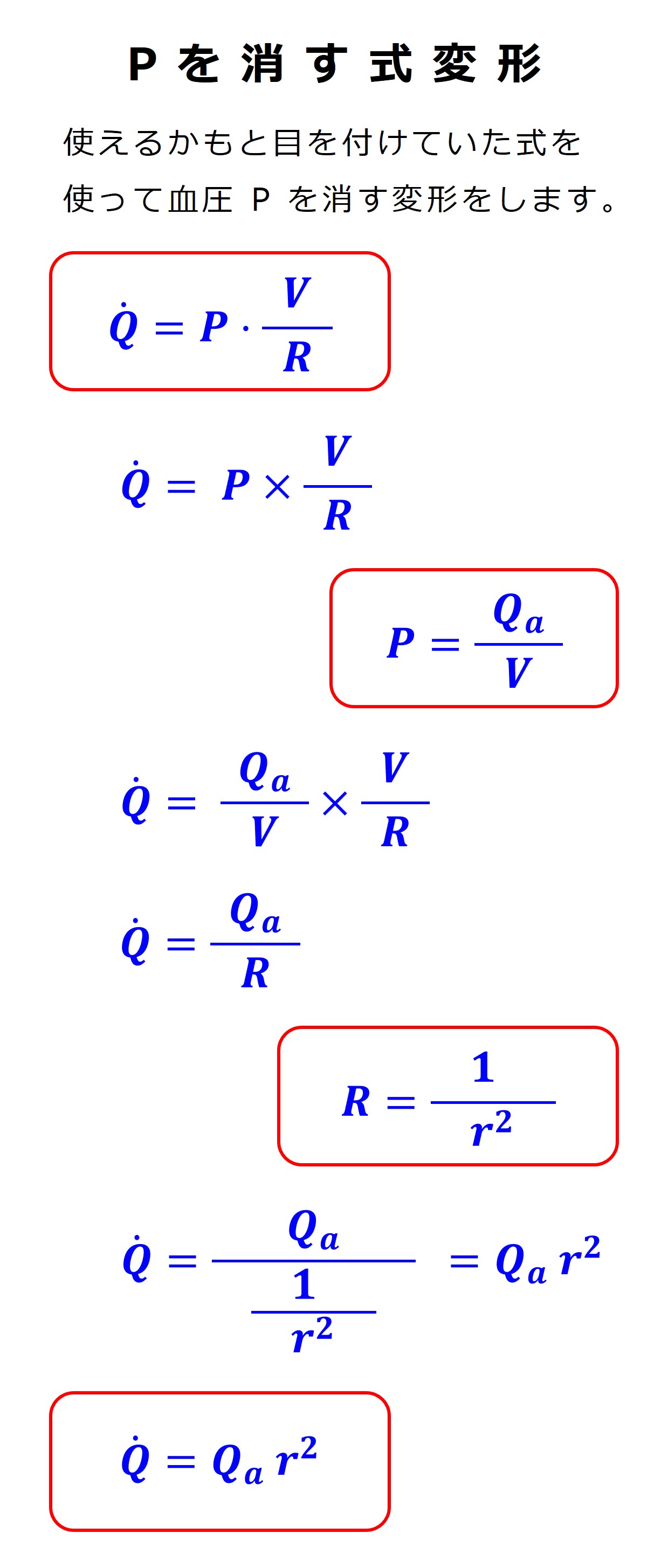
血管径の変化が血流量に及ぼす影響を見るために、数式をもっと変形して血圧 P を消してみましょう。
そのためには、そもそも「圧力って何?、温度って何?」という物理学的な疑問から出発してもよいのですが、とても長く険しい道のりとなるので、ここでは高校で学ぶ「物体の状態方程式」というものを利用します。
日本の中学校では ボイルの法則(気体に圧力をかけていくとその大きさに反比例して体積が小さくなる)や シャルルの法則(一定の圧力下で気体を温めると絶体温度の上昇に比例して体積が大きくなる)を教わります。
高校では「理想気体の状態方程式」というのを学びます。
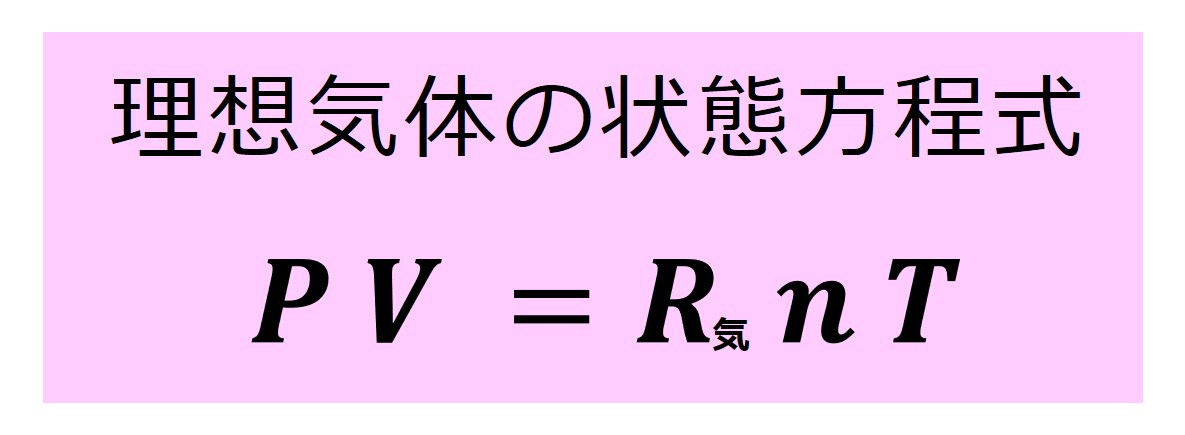
ここでの R気 は気体定数と呼ばれているものです。
実在気体に対しては「ファン・デル・ワールスの状態方程式」というものがありますが、圧力 P 、体積 V 、温度 T 、物質量(粒子数 n )の関係を示す基本的な形は「理想気体の状態方程式」と似ています(参考:便宜的導出?)。
「ファン・デル・ワールスの状態方程式」は、液体でもある程度利用可能とされているので、圧力、体積、温度、物質量(粒子数 n )の基本的な関係そのものは液体でも似たようなものだと考えられます。
基本的な関係は似ていると期待できますが、気体に比べると液体は分子間の相互作用がとても強く、「圧力、体積、温度」の実際の関係はかなり複雑なようです。
液体は圧力変化や温度変化に対する体積変化が気体よりはるかに小さく、実験で調べるのも難しいようです。
特に血液は複雑な要素の集まった混合液体なので、「圧力、体積、温度」の関係を数式で表すことはほぼ不可能でしょう。
ほとんどお手上げ状態ではありますが、「理想気体の状態方程式」に見られる「圧力、体積、温度の基本的な関係」は多少頼りにできそうなので、それを利用することにします。
「理想気体の状態方程式」を利用して得られた結果が、臨床で経験的に得られる生理学的な実情と合っていれば「ラッキー 😀」、多少のご利益はあったということにしましょう。
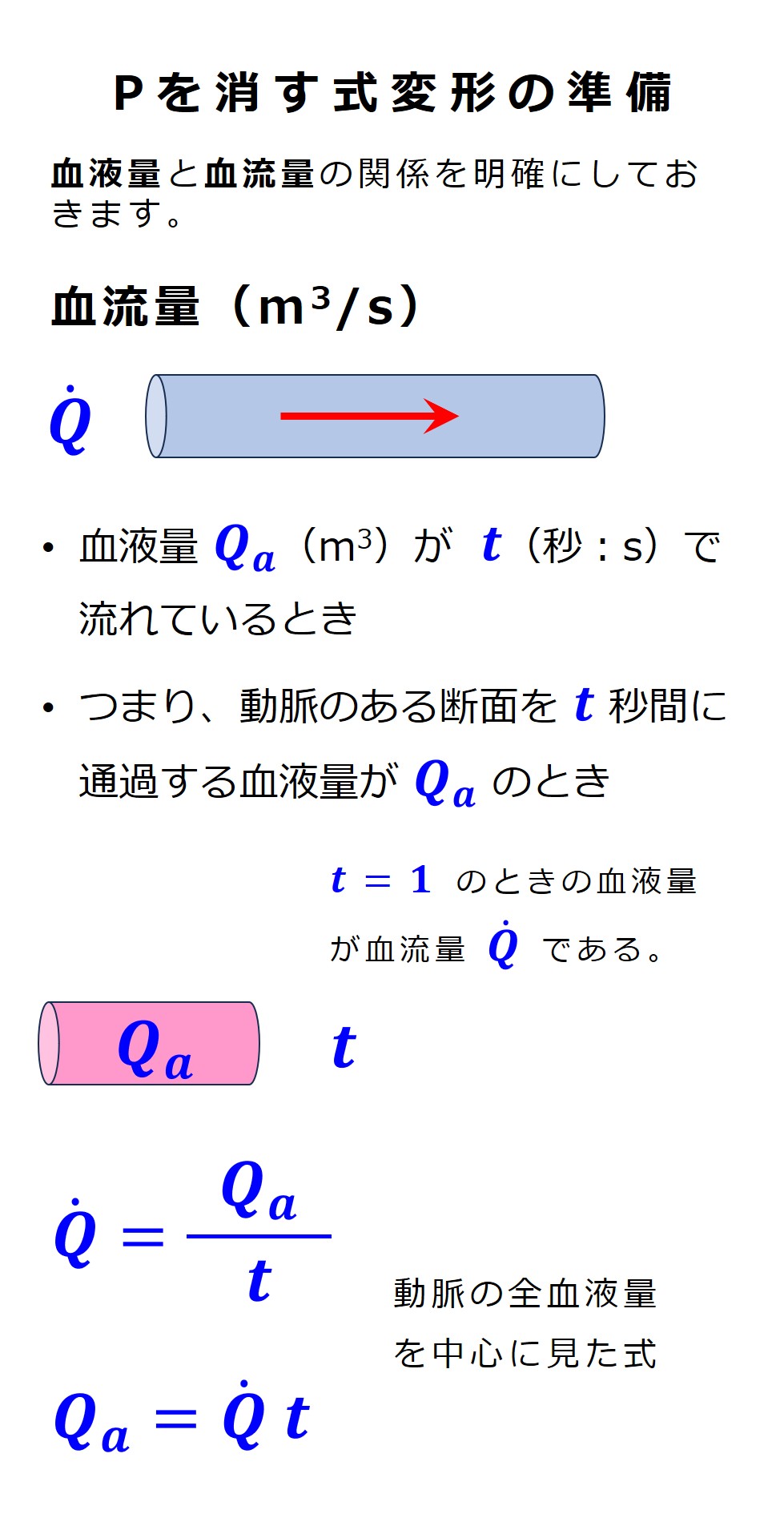
大事なのは血流量 Q です。血流量を推し量る計算式 から血圧 P を消しましょう。
けっこう、乱暴にいきます。

ここではポケモン「バサギリ」の支援を受けています。



先に見たページに戻るときは、リンクを使うよりも、ブラウザの「<(もどる、Back)」を使うと通信量を節約でき、また早く表示されます。
医者の不養生:一喜一憂しない血圧管理