医者の不養生:一喜一憂しない血圧管理
先に見たページに戻るときは、リンクを使うよりも、ブラウザの「<(もどる、Back)」を使うと通信量を節約でき、また早く表示されます。
さて、これまで見てきたように、ハーゲン・ポワズイユの法則 は、実際の血管で使うには変数が多すぎるので、これから思い切って削れるものを削り落として、簡略な数式に加工します。
覚えやすい形に加工できれば役に立つようになります。
ここで求めていくのは、「目の前の血圧 80/50 mmHg の患者に 30 分 かけて 500 mL の輸液をおこなえば、血圧が 100/60 mmHg になるだろう」といった数値計算による予測のできる数式ではありません。
(mmHg:水銀柱の高さで圧力を表しています)
(注:mL:ミリリットル;臨床で実際に使われている単位を使用しています)
「輸液をおこなえば血圧は上がるはずだ」と予測できればそれでよいのです。予測に反して血圧が上がらない時は原因を探ることになります。そういう意味での実用性がある「変化の向きのわかる数式」を求めていきます。
ここでは 重要な変数間のざっとした関係性 だけを見ていくので、次の方針で余計なものを削り落としていきます。
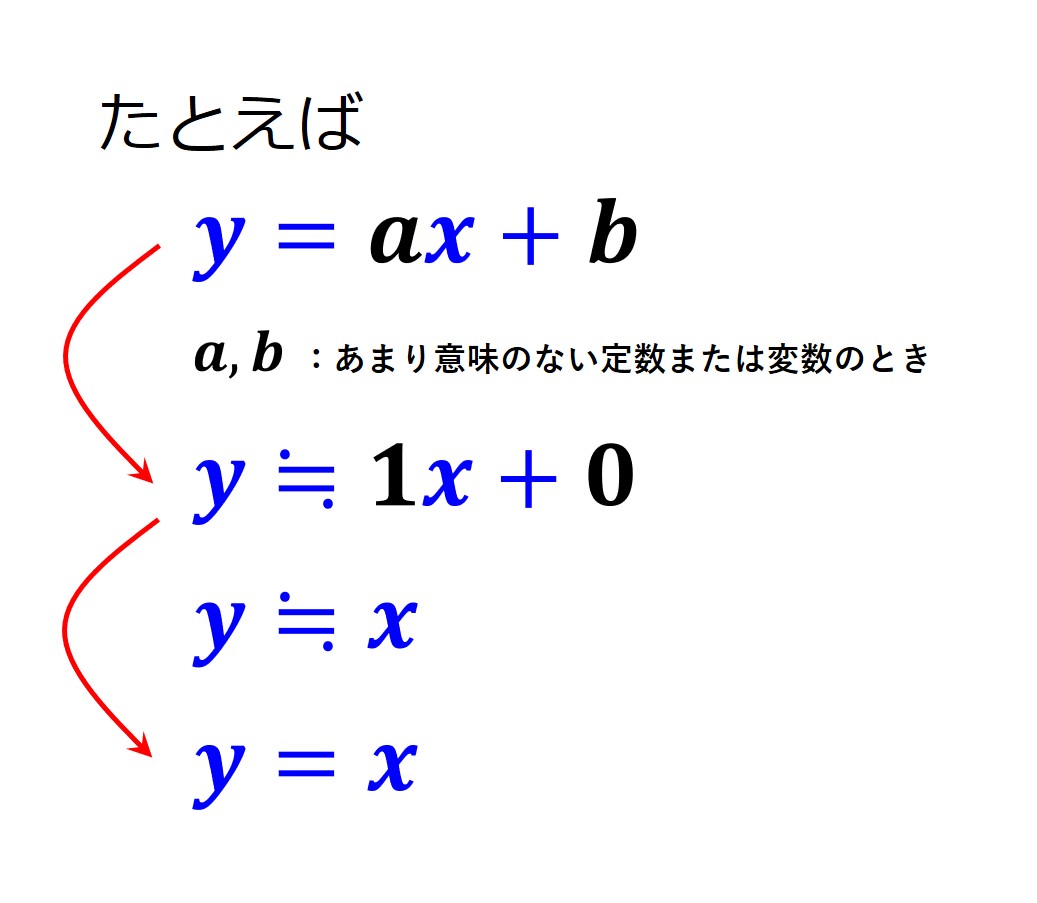
最初は隠した係数などを意識して「∝」や「≒」を使うかもしれませんが、すぐ「=」にします。

以上の方針で、かなり乱暴に ハーゲン・ポワズイユ の数式を叩き壊していきます 😁
では、式の変形・簡略化を見てください 👹



実際の動脈における血圧波形の変化は、下図のような感じです(雑なイメージ図)。
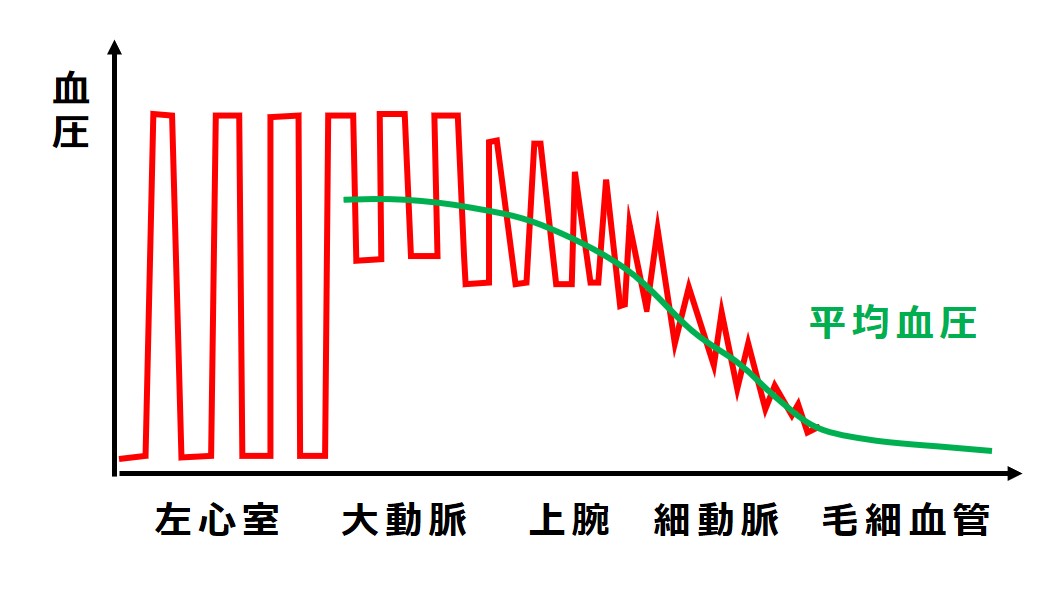
「Blood Pressure: From the Aorta to the Capillaries」でネット検索するといろいろな図を見ることができます。



分母のゴチャゴチャしたのをまとめて R としましたが、この R の数式は「乙式(R''')」です(8 → 1 になっています)。

この先、役に立ちそうな数式をピックアップしておきます。

定数の「8」、粘性 η(イータ)、L(血管の長さ)など、全部「1」としました 😄
ドロドロ血液だと血液の粘性 η(イータ)が大きくなります。血液はサラサラが良いでしょう。
ここでは血液の粘性 η(イータ)も「1」とみなして、消してしまいます。
圧力は P1 しか使わないので、もう P と表記します。
円周率 π は「1」に出来ませんでした。
式変形の途中を省いて、大事そうな式だけをまとめておきます。

思い切った簡略化で重要な式がいくつか得られています。
でも覚える必要はまだありません。
最後の式「 Q = P π r 4 」「血流量 = 血圧 ×3.14… ×(血管径の4乗)」が気になりますね。
血管の径が2倍に広がっても、血流量が 24=16倍に増えるわけではありません。
径が2倍に大きくなると血管内腔の容積は 22=4倍に大きくなります。
しかし、すぐに血液が充填(じゅうてん)されて4倍になるわけではないので、血圧 P は低下します。
血圧 P 、ちょっと邪魔ですね。😠
先に見たページに戻るときは、リンクを使うよりも、ブラウザの「<(もどる、Back)」を使うと通信量を節約でき、また早く表示されます。
医者の不養生:一喜一憂しない血圧管理
Insane! @kealakennelly at The Eddie yesterday. Despite struggling with mental health and physical injuries from previous big wave wipeouts, KK showed 100% commitment, turned and went...total respect KK, you're a legend.
— SurfGirl Mag (@SurfGirlMag) January 23, 2023
Footage @peterkingphoto pic.twitter.com/sqpScBuE7A
Eddie Aikau Big Wave Invitational 2025#Surf #Waimea #Hawaii pic.twitter.com/To1g8h3UJR
— carinha que mora logo ali 🏄♂️🎸 (@_magoo) December 28, 2024